Музыка и математика: почему меняется звук гитарных струн, чем отличается высокая «ля» от низкой, и зачем композитору 3D-пространство гармонии

Античная баллада и современная музыка, классическая симфония и популярная песня в караоке — все музыкальные произведения похожи больше, чем может показаться на первый взгляд. Они состоят из звуков, или «атомов» музыки, которые выстраиваются в последовательность по определенным правилам. Как именно звуки складываются в линейную мелодию и пространственную гармонию, что такое октавы и как с ними связаны знаменитые до, ре, ми и остальные ноты — в материале «Энергии+».
Когда гитарист дергает струну, она начинает дрожать (колебаться). Это колебание передается молекулам воздуха, а от них — на барабанные перепонки. Распространяющаяся в воздухе и достигающая наших ушей волна и есть звук. Слышим мы его не всегда. Если колебания будут «медленными», наши уши не зафиксируют сигнал. Например, скакалка в руках у прыгающего на ней ребенка делает 1–2 оборота в секунду, и звука не возникает. Но если раскрутить ее быстрее, мы услышим характерный свист.
Число повторений в единицу времени называется частотой. Она измеряется в герцах: один герц — это одно повторение в секунду. Человеческое ухо воспринимает в качестве звука колебания с частотами от 20 до 20 000 герц, то есть когда гитарная струна за секунду колеблется от 20 до 20 000 раз. Чем больше частота, тем выше звук.
Высота звука обратно пропорциональна длине струны: чем короче струна (при неизменной толщине и натяжении), тем выше звук. Именно частота меняется при зажатии аккорда на струнах гитары. Струны внутри рояля, издающие высокие звуки, изначально короче тех, что дают низкий басовый звук.

Ярослав Тимофеев
музыковед, композитор, преподаватель в Музыкальной мастерской Юрия Розума
Рояль — это струнный инструмент. Когда музыкант нажимает клавишу, это движение через несколько рычагов передается молоточку — деревянной палочке с войлочным наконечником. Он ударяет по металлической струне, колеблет ее, и получается звук с частотой, зависящей от длины и толщины струны.
В музыке, как правило, используют 88 частот, лежащих между 20 и 20 000 герц. Все музыкальные инструменты издают звуки только из этого набора. Представьте себе пионерский лагерь, в котором отдыхают 88 детей. Во всех играх — футболе, прятках, шахматах — будут участвовать только эти дети. Необязательно все сразу, например в футбольном матче задействованы 22 игрока, а в шахматной партии — только два. Баллады, симфонии, песни — это «игры», организованные директором «лагеря» — композитором. Чтобы мелодия пришлась слушателю по вкусу, композитор должен знать, какие звуки «дружат» между собой, а какие — нет. Но перед этим их нужно поделить на «отряды».

Фортепиано: линейная мелодия
Детей в лагере на линейке расставляют по росту. Если 88 звуков выстроить в одну линию от самых басовых до самых звонких, получится фортепиано. Каждая его клавиша издает звук определенной высоты. Слева звуки низкие, справа — высокие. Разница в «росте» между соседними клавишами всегда одинаковая и называется полутоном.
На клавиатуре фортепиано повторяется фрагмент из семи белых и пяти черных клавиш. Этот диапазон называется октавой. Как будто детей в лагере разбили на отряды. У каждого ребенка в отряде своя роль: дежурный по кухне, ответственный за спорт, творчество и т.д. Названия «ролей» в октавах — это ноты.
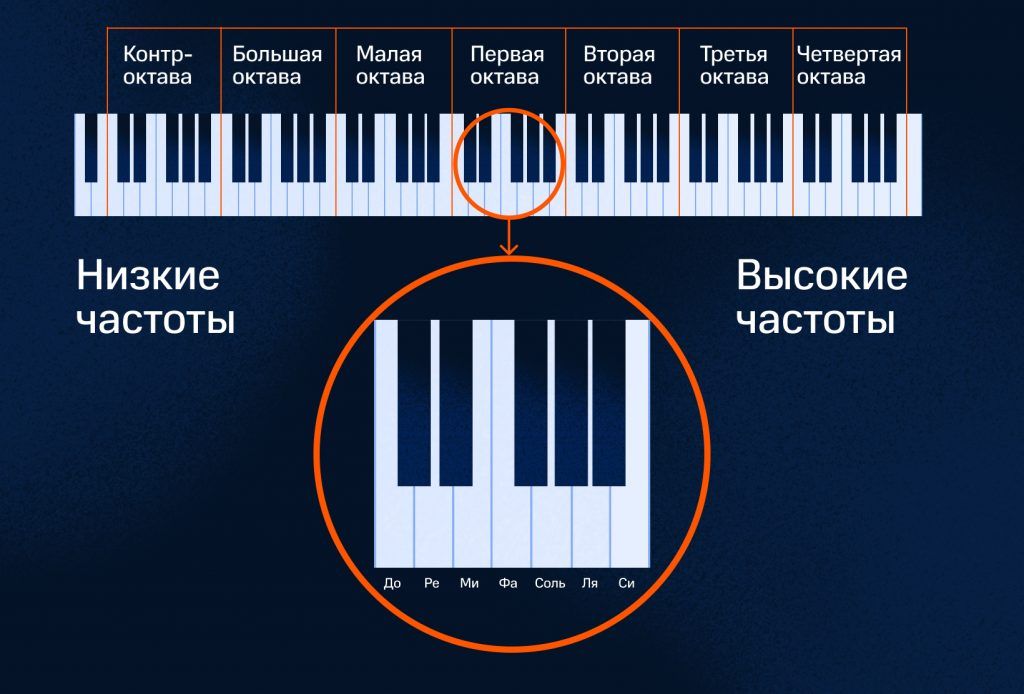
На белых клавишах расположены звуки с нотами — до, ре, ми, фа, соль, ля, си. Еще их обозначают латинскими буквами – c, d, e, f, g, a, h. В октаве есть и черные клавиши. Их называют по соседним белым с использованием символов диез (#) — знак повышения звука на полтона, и бемоль (b) — знак понижения на полтона. Клавиша между до и ре называется до-диез или ре-бемоль. Звуки, расположенные на соседних клавишах, «ладят» плохо. Так и дети, стоящие рядом на линейке, необязательно друзья.
«Недавно я сочинял музыку для мюзикла «Восемь женщин», — поделился Ярослав Тимофеев. — В финале героини превращаются в фурий — карающих страшных существ. Я взял восемь нот подряд — это содержимое октавы (такой набор называется гаммой) — и построил на них финальный номер спектакля. Ноты символизировали героинь, которые правят миром, как гамма правит миром музыкальных звуков».
Названия нот повторяются во всех октавах. Чтобы указать конкретную ноту из 88, говорят ее название и принадлежность к октаве: «до первой октавы» или «ля контроктавы». Одноименные ноты в разных октавах, например ля первой октавы и ля второй октавы, гармонично сочетаются между собой и звучат красиво, если сыграть их одновременно. Дело в том, что октавная связь — первая и самая крепкая между звуками, а объясняет эту связь математика. Нота ля первой октавы звучит на частоте 440 герц, ля второй октавы — на 880 Гц. Соотношение частот этих двух звуков 1 к 2. Почему именно при таком соотношении получается приятное созвучие? Все дело в структуре звука.
Гармония: почему звуки «дружат»
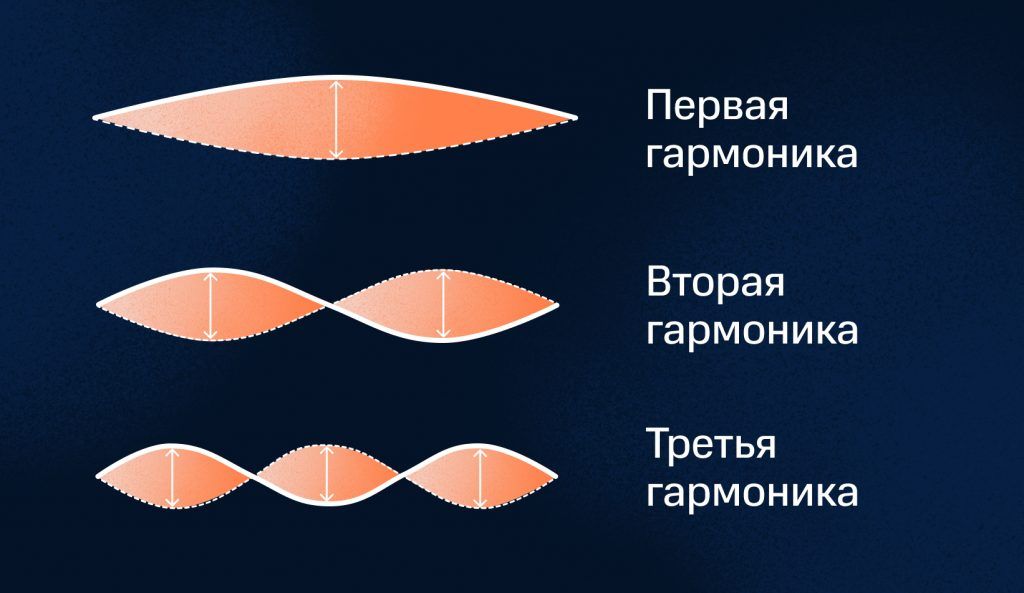
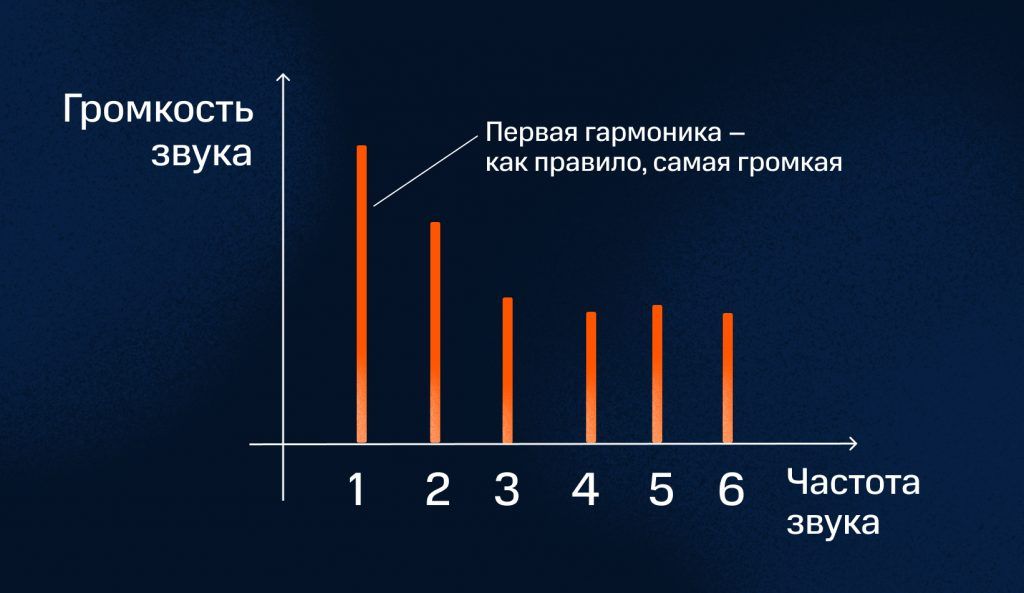
Когда музыкант ударяет по струне, на самом деле рождается не один звук, а сразу несколько. Все потому, что колебание струны в пространстве — сложнее, чем просто движение «туда-сюда». Колебание, дающее звук, состоит из «суммы» колебаний, каждое из которых вносит в итоговый звук свой вклад — гармонику. Как правило, чем проще «форма» колебания, тем громче и ниже гармоника.
При колебании струны «целиком» издается первая гармоника, или основной тон: самый громкий. Именно его обычно подразумевают, когда говорят, что струна издает звук. В случае с нотой ля первой октавы частота такого колебания и будет равна 440 герцам. Но в тот же самый момент струна изгибается, как две половинки, издавая звук в два раза выше — вторую гармонику. Одновременно струна изгибается тремя полуволнами, производя звук в три раза выше (третью гармонику). Вместе с тем — четвертую, пятую, шестую, и так до бесконечности.
Чтобы лучше понять, как возникают гармоники, представим девочку, скачущую на скакалке. Девочка подпрыгивает, затем приземляется и снова подпрыгивает. Это простое движение «вверх-вниз» похоже на колебание струны, порождающее первую гармонику. Пышное платье на девочке колеблется несинхронно с ее прыжками: за один прыжок легкая ткань успевает подняться и опуститься два раза. Колебание платья — это вторая гармоника. На платье привязаны ленточки из еще более летящей ткани: они колеблются в три раза быстрее, чем прыгает девочка. Это третья гармоника. В случае со струной, гармоник бесконечно много, и каждая звучит все тише.
Две девочки в лагере могут быстро найти общий язык, обсуждая свои похожие платья и ленточки на них, а звуки хорошо сочетаются, если у них много общих гармоник. Когда второй звук ровно в два раза выше, чем первый, у звуков совпадает каждая вторая гармоника — у них очень много общего. Поэтому октавная связь и считается самой сильной. Есть и другие соотношения, называемые базовыми интервалами, когда второй звук в три и пять раз выше исходного. В этих случаях у звуков совпадают каждая третья и пятая гармоники, соответственно. Для ноты ля первой октавы это будут звуки с частотами 1320 и 2200 герц, то есть ноты ми третьей октавы и до диез четвертой.
Числа 2, 3 и 5, на которые умножают частоту исходного звука, выбраны неслучайно: это простые числа. Умножение на 4 не входит в базовые интервалы, так как 4 = 2*2, этот интервал можно получить, дважды умножив на 2, — это производный интервал. Теоретически можно использовать кратность — умножение на 7, но в классической и современной музыке такие звуки (и интервалы, ими образованные) не используются. Возможно, они встретятся в музыке будущего.
Трехмерное пространство музыкальной гармонии
Опытный директор детского лагеря, заглянув несколько раз в столовую, понимает, какие дети будут дружить, а какие — вечно ссориться. Композиторы могут увидеть все гармонические связи между нотами в особой трехмерной системе координат, которая называется пространством кратностей. На пересечении трех координатных осей, в начале координат, располагается исходная нота (до). По каждой оси отложена своя кратность: умножение на три, на пять и на два (октавы).
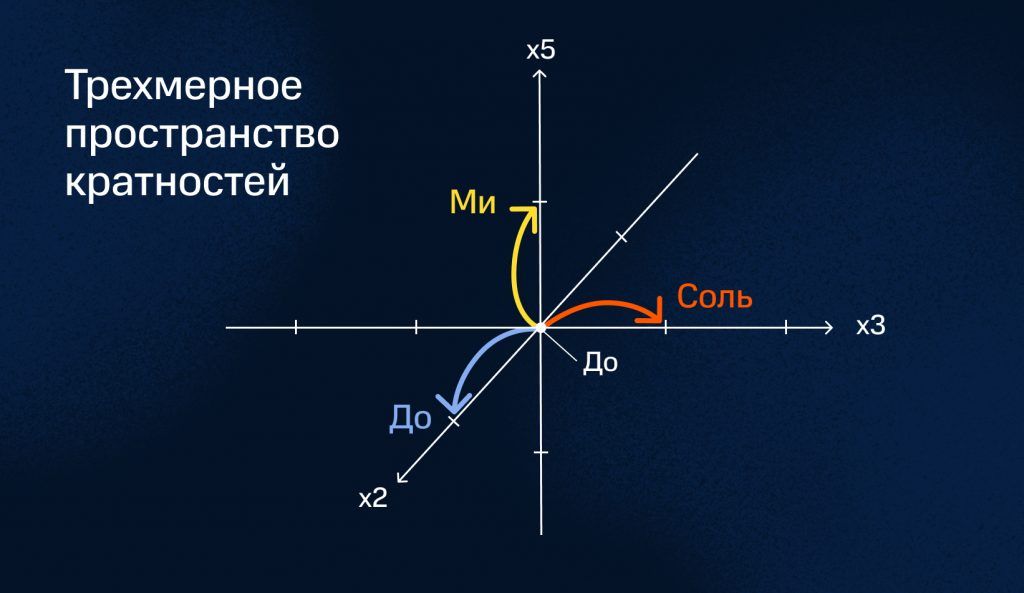
Делая от центральной ноты шаги в каждом направлении, композитор попадает на какие-то музыкальные звуки в каждом узле этого пространства. Чем ближе звуки в пространстве, тем гармоничнее и приятнее они звучат вместе. Чем больше шагов нужно сделать от одного узла к другому, тем меньше у этих звуков останется общих гармоник и тем менее благозвучное сочетание они дадут.
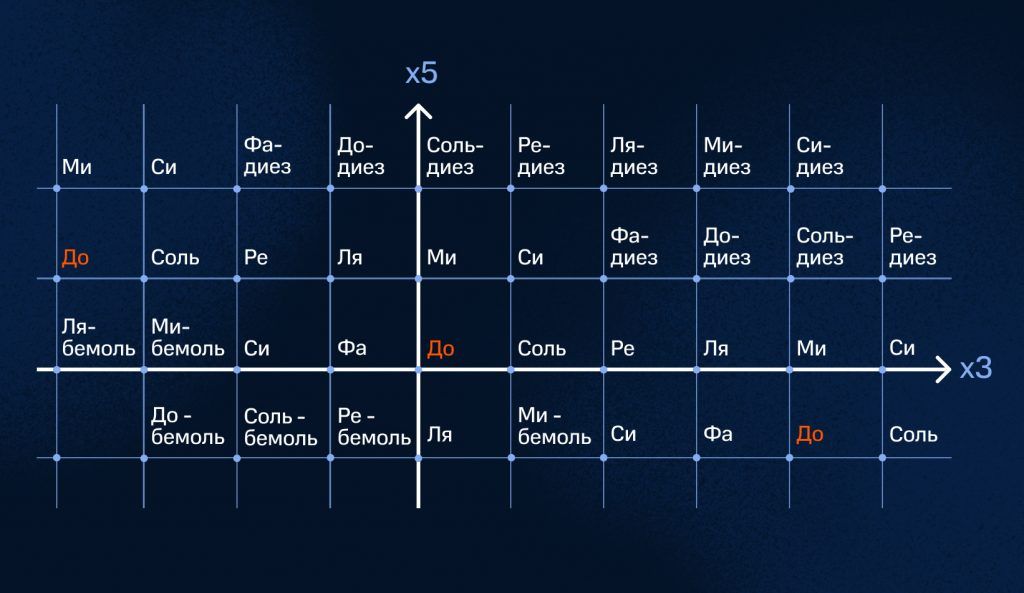
Если поставить в начало координат, например, ноту до и рассмотреть только две оси, отвечающие за умножение частоты на 3 и на 5, можно увидеть названия всех звуков, используемых в музыке, и гармонические связи между ними. Как будто ребята из пионерского лагеря выстроились не по росту, а по тому, насколько они дружны между собой. Ориентируясь в пространстве музыкальной гармонии, композитор сразу увидит, какие звуки отправить в одну «команду», например аккорд или тональность, чтобы создать математически выверенное музыкальное произведение.
«Еще Пифагор сказал, что музыка — это наука о звучащих числах, а древние греки объясняли законы музыки через движение планет, — рассказал Ярослав Тимофеев. — В античном мире верили, что каждая планета издает собственный звук, а люди не слышат его, потому что он слишком… громкий. У звука каждой планеты был свой аналог в мире музыкальных интервалов. Сейчас законами астрономии музыку не объясняют, а вот тезис о «звучащих числах» полностью подтвердился: доказано, что в основе музыкальной гармонии лежат математические законы. Без соблюдения этих законов хорошее музыкальное произведение сочинить вряд ли удастся».












